Hello pals,

In this article, I will explain the importance of the BIP-32, BIP-39 and BIP-44 standards and how they are fundamental to the functionality of wallets like MetaMask.

To ensure a clear understanding for most readers, we will start with a brief overview of what BIPs are, what wallets are, and the different types of wallets that exist.

From there, we will dive deeper into how wallets use the standards mentioned above to manage cryptographic keys effectively.

1. What Are BIPs (Bitcoin Improvement Proposals)?

In a simplistic way, BIPs are documents that propose technical improvements or other types of enhancements for the development of Bitcoin.

Each BIP has an associated number and includes a clear, concise explanation along with a justification for the new feature.

2. Are BIPs Only for Bitcoin? Why Are They Used in Ethereum?

Although BIPs were originally created for Bitcoin, some of them have become fundamental to the blockchain ecosystem.

BIP-32, BIP-39, and BIP-44 are not exclusive to Bitcoin. They provide the documentation on how HD wallets should generate and manage their private keys in a structured and secure way.

Other blockchains have adopted these standards, which is why it is now common for many wallets to follow them, ensuring consistency in key management across different wallets.

3. What is a Wallet?

In the real world, a wallet is basically a pouch, a case, or any other small container where we keep documents, coins, banknotes, or other valuable items.

In the blockchain space, wallets serve a similar purpose—they store valuable digital assets.
However, instead of physical items, a blockchain wallet is a software responsible for storing private and public keys.
It also manages these keys and allows the wallet owner to interact with the blockchain, such as signing transactions, verifying balances, buy NFTs etc...

You might be wondering, if crypto wallets only hold the keys, where does the current balance come from?
Wasn’t it supposed to store the tokens as well?

Yeah, for those just getting started in Web3, this is a pretty common question. (I asked myself the same question in the past! 😅)

For example, when you check your balance on MetaMask or another wallet, that balance is actually calculated based on past transactions. The wallet itself queries the blockchain to retrieve this data, allowing you to see your balance.

The tokens themselves only exist on the blockchain, not inside the wallet.

This makes the wallet just an interface that communicates with the blockchain.

Well, pals, that’s a wallet in a nutshell! There’s actually a lot more to know about wallets, but I won’t dive deeper now to avoid going out of the scope of this post.
Maybe I’ll explain it in another post later!

4. Types of Wallets: Deterministic vs. Non-Deterministic

There are two types of wallets whose differences are based on whether the generated keys are related to each other or not.

4.1 - Non-Deterministic Wallets (ND Wallets) – The Old Method

A Non-Deterministic Wallet ( ND Wallet ) is a type of wallet where each key is generated randomly, and these keys have no relationship with each other.

In this type of wallet, sometimes a new key was created for every transaction.

This brings some downsides, such as the need to backup each key every time a new one is generated.

At some point, this would become impractical and difficult to manage.

If the user, for some reason, loses the private key or the device where the private keys are stored, access to the funds would be permanently lost with no way to recover them, since the generated keys were completely random and not derived from a single source.

Nowadays, this type of wallet is deprecated and is no longer an industry standard due to its inefficiencies and risks.

 4.2 - Hierarchical Deterministic Wallets (HD Wallets) – The Modern Solution
In contrast, there’s another type of wallet that replaced Non-Deterministic Wallets (ND Wallets) and became the industry standard.

We’re talking about Deterministic Wallets, also called HD Wallets (Hierarchical Deterministic Wallets).

In this type of wallet, the generated keys are derived from a single source (the master key or seed phrase).

One major advantage of these wallets is that no matter how many keys you generate, you can always recover all of them as long as you have access to the master key or seed phrase.

This brings even more advantages, as you don’t need to back up each key individually every time a new key is generated—all keys are mathematically related to the seed.

The OG's BIP-32 , BIP-39 and BIP-44 are the standards that enable the technology behind HD Wallets, and we will explore them in detail later.

5. The Role of BIP-32

 5.1 - What is BIP-32?

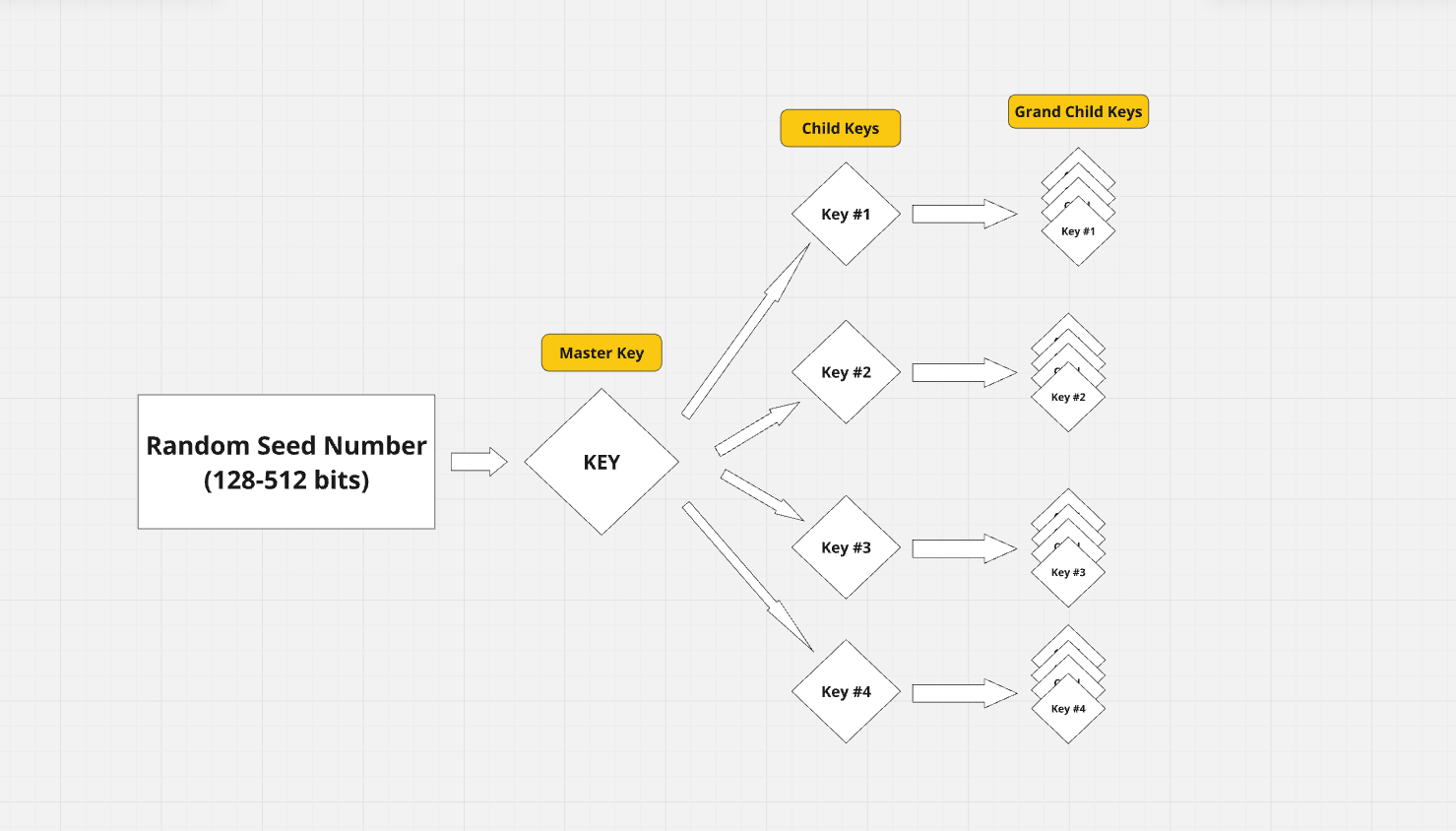
BIP-32 is a proposal that states that, from a single random seed (typically a random number between 128 and 512 bits), we can derive a sequence of keys in a hierarchical tree structure.

The child keys are derived using specific mathematical operations, which I prefer to explain in more detail in a separate post.

These derived keys, in turn, can derive other child keys, enabling hierarchical deterministic (HD) wallets.

Below is an image that represents the tree of keys generated from a single seed.

This tree structure can be used for organizational purposes.

For example, in a hypothetical situation, the first branch could be used to deploy smart contracts, the second branch to send funds, and the third branch of keys to only receive payments.

Given that the tree of keys can reach a significant depth, we can organize the use of the branches according to our specific needs. In practical scenarios, each branch can represent different accounts or functionalities, making it easier to separate and manage activities, such as handling multiple users, services, or specific blockchain operations.

 5.2 - Hardened Key Derivation vs Soft Derivation

There are two ways to derive keys in the tree hierarchy:
Hardened Key Derivation and Soft Derivation.

I gotta admit that most people struggle to understand these specific derivation concepts, given that they become clearer once you understand the math behind them.

I will do my best to explain it to you without bothering you with crazy math because the goal here is for you to understand the difference between them.

Let’s start with the first one: Soft Derivation.

In soft derivation, both private and public keys are extended using an algorithm that allows both master keys and child keys to be used to derive new child keys.

The derived keys (public and private) that are in the same specific position in the derivation tree are mathematically correlated. This introduces security risks because if certain elements of the derivation (such as the chain code and the index) are leaked, an attacker could potentially compute the master public and private key, meaning you can say goodbye to your coins. 🙁

Because of these risks, most HD wallets use another type of derivation called Hardened Key Derivation.

In this type of derivation, the private key is extended using a different algorithm, where the derivation depends only on the master private key. Unlike soft derivation, child keys cannot be used to derive further child keys.

Even if the chain code and the index of a derived key are leaked, the attacker will not be able to retrieve the master private key.

5.3 - What about Hardened Key Derivation for public keys?

If you noticed, I didn’t talk about the use of Hardened Key Derivation for public keys.

That was on purpose because, as I said before, in soft derivation, the derived public keys are correlated with the private keys if both keys are in the same position in the derivation tree.

This allows developers to deploy some apps in read-only mode, while at the same time, they can deploy other apps that will be responsible for managing funds, given that the keys are correlated.

When using Hardened Key Derivation, it doesn’t make sense to apply it to public keys because it’s impossible to get the correlated private key, even if we have the chain code and the index of the key in question.

Hypothetically, if a developer used Hardened Key Derivation for public keys and by accident some funds are sent to these public addresses, the funds would be lost forever, unless we borrow some quantum computers from Google to recover the private keys by brute force. 😝😝😝😝😝

So, in conclusion, Hardened Key Derivation makes more sense when we want to generate private keys, which is mostly used in the context of creating new accounts.

5.4 - The derivation path
In order to identify the keys in the HD wallet, a path naming convention is followed.

The convention is very straightforward to understand:

• Each level is separated by a slash character (/).
• The first level in the naming convention starts with the letter “m” (lowercase for keys derived from the master private key) or “M” (uppercase for keys derived from the master public key).
• We should read the path from left to right.
  

Let me show you some examples so you can understand it better.

m/0 - The first (0) child private key of the master private key(m)

m/2/1 - The second grand child private key of the third child

m/2'/0 - The first normal grand child of the third hardened child

M/2/1 - The second grand child public key of the third child

I think these examples were more than enough for you to understand how the path naming convention works for derived keys.

In the examples above, the index of some hardened child keys contains an apostrophe next to it.
That's how the hardened indexes are represented.

In the path below, 2' means the third hardened level, and as you suspect, 2' is not the real index and must be something else.
m/2'/0 - The first normal grand child of the third hardened child

Before I tell you what the real index is, let me tell you that for normal derivation, the index numbers range from 0 (0x0) to 2^{31} - 1 (0x7FFFFFFF), and for hardened derivation, the index numbers range from 2^{31} (0x80000000) to 2^{32} - 1 (0xFFFFFFFF).

So, to calculate the real index of 2', we should do the calculations below:

2 + 2^{31} = 2147483650

and as a result:

m/2'/0 = m/2147483650/0

As you can see, it is not user-friendly to read such a large number, which is why hardened indexes are represented in a different format.

6. The Role of BIP-39

 6.1 - What is BIP-39?

It’s known that, for security reasons, there are some measures that must be taken into account when backing up private keys.

One of the most important measures is to avoid saving it electronically, like sending the key to a cloud service or by email, for example.

So, the old-fashioned way of saving it on paper is still the most preferred method.

But now imagine writing the private key on paper, letter by letter, in a case-sensitive way.

There’s a risk that, if you uppercase a character by mistake, when trying to import your account into a wallet, you might encounter a situation where you can’t access your account. The hard part? You would have to go through a trial-and-error process to figure out which character is incorrect or which one should have the proper case.

Well, you can imagine the serious burden that would be, right?

Thankfully, our saviour, the great OG BIP-39 is here to help! 😜

BIP-39 is a standard that states that, given a high source of entropy where we can generate a random number between 128 and 256 bits, we can encode that random number into a sequence of code words (12 to 24 words).

These code words are more than sufficient to create the seed key and, in turn, generate all the derived keys.

And, of course, these words are much easier to write on paper, given that they are always in lowercase and simpler compared to a randomly generated key.

There are folks who spend time memorizing the mnemonics due to the simplicity of the code words. (Kudos to them!)

By having this sequence of code words, we can import them into a deterministic wallet like MetaMask in order to generate the derived keys.

Imagine that you are using the MetaMask wallet extension, and you have already created 10 accounts. For some reason, you just bought another computer and want to import the same 10 accounts.
The first thing you should do is export the mnemonic words to a secure location.
Now, on the new device with a compatible HD wallet installed, you just need to import the mnemonic words and manually create the accounts by selecting the 'Add Account' button (or a similar option) 10 times until you recover all your accounts.

In these HD wallets, the account creation process follows the same algorithm and order.
This means that if you create 10 accounts in MetaMask on one device, the same 10 accounts will be created in another wallet if you import the same mnemonic words and add them manually as mention before.

In some extreme situations where you have already generated thousands of accounts in another wallet and want to import them into a different wallet, using a script would likely be the smartest approach.

With all this said, I think this explains why the crypto industry decided to adopt the BIP-39 as a standard.

In a nuthsell you can back up your entire hd wallet, by importing the mnemonic words in a compatible HD wallet.

6.2 - How the mnemonic words are generated?

Let’s go through the step-by-step process of how these mnemonics are generated.
What you’re about to see is what really happens behind the scenes when you create a new account for the first time in the majority of deterministic wallets (e.g., MetaMask, Phantom, Trust Wallet, etc.).

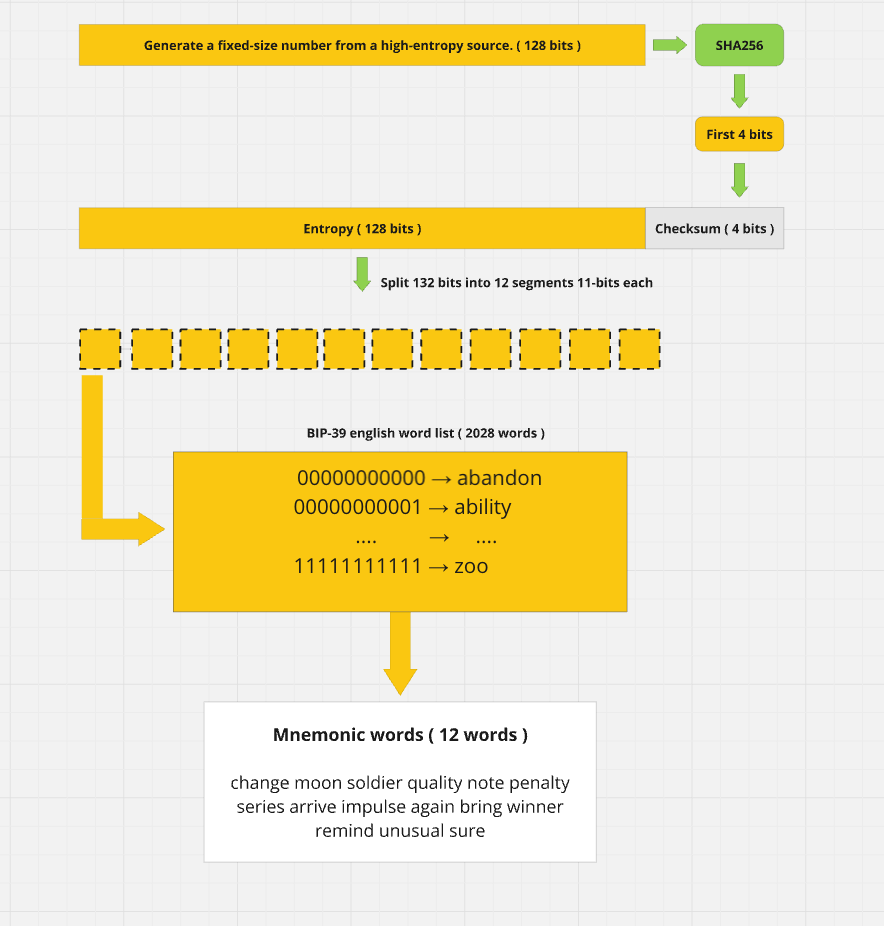
• Generate Random Entropy
  • The first step is to generate a random number of a fixed size from a reliable source of entropy.
    The size of this entropy is directly correlated with the number of words that will be generated in the mnemonic.
    
    For example:
    
    128 bits → 12 words
    182 bits → 18 words
    256 bits → 24 words
    
•  Calculate Checksum (SHA-256 of Entropy, First N Bits)
  • Calculate the SHA-256 hash of the entropy.
  • Extract the first N bits from the hash to use as a checksum.
  • N is calculated by dividing the size of the entropy by 32.
    
    Example:
    If the entropy size is 256 bits, N will be 8 (256 ÷ 32).

• Concatenate Entropy + Checksum
  • The original entropy is concatenated with the checksum, resulting in a sequence of bits that is a multiple of 11.
• Divide into 11-bit Groups
  • The previous concatened seuence is divided into groups of 11 bits
    We map to 11 bits because the BIP-39 word dicitonary contains 2048 words , that means, 2¹¹ = 2048.
• Convert to Words Using the BIP-39 Dictionary
  • Each group of 11 bits is mapped to a corresponding word in the BIP-39 dictionary.
    
    Example:
    The sequence 00010110010 in decimal is 178, which would map to the word "apple" in the BIP-39 dictionary, and so on.
    
• (Optional) Add a Passphrase
  
  • You can add a passphrase to enhance security. However, keep in mind that if you lose the passphrase, it will be impossible to recover the account, even if you have the correct mnemonic words.

At the end of these steps, the mnemonic phrase will be successfully created.

You can use these steps as homework to implement a basic mnemonic generator. 😋

If you still struggling understanding the mnemonic generation steps, below a visual represenation to make things more clear:

6.3 - How the seed key is generated from the mnemonic words?

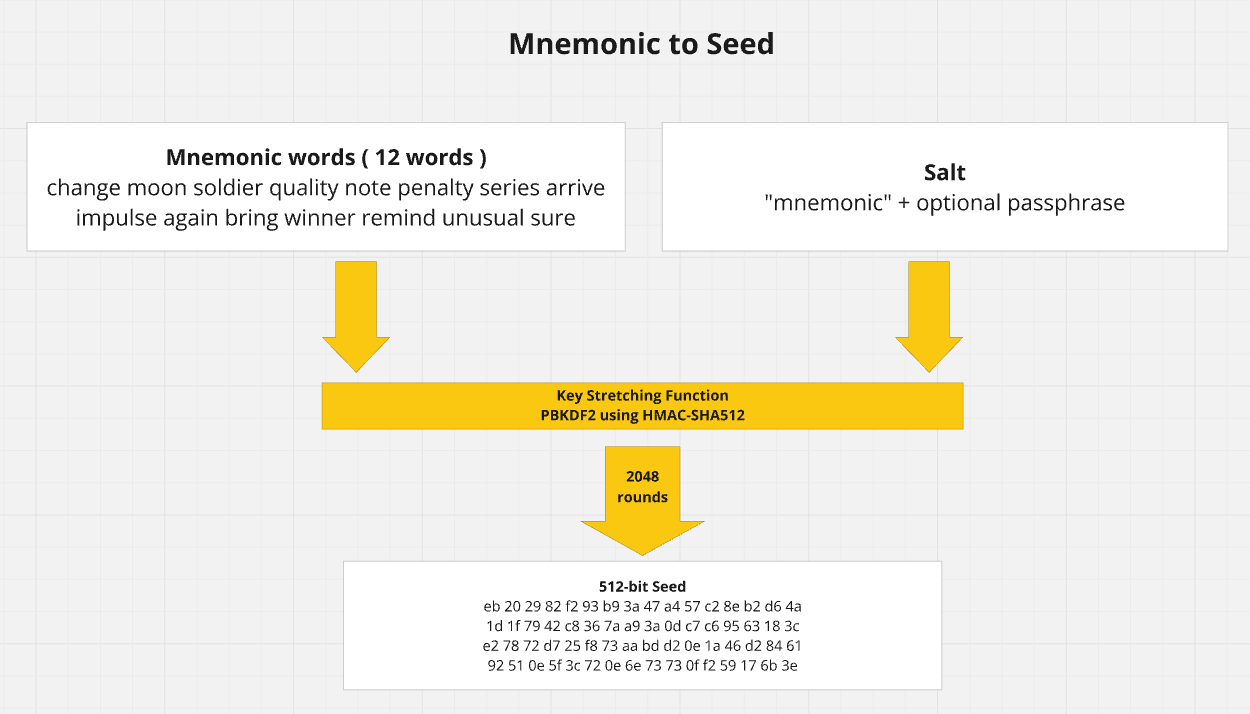
To generate the seed key from the mnemonic you need to use the stretching function PBKDF2.

PBKDF2 is an hashign algorithm and if you want to know more about it click in the link below
https://nishothan-17.medium.com/pbkdf2-hashing-algorithm-841d5cc9178d

This function takes 2 parameters, the mnemonic and the salt.

the salt is optional and allows you to introduce a passphrase.
As i said before, if you loose the pasphrase its impossible to revoer the account even igf you have the proper menmonic words.

Additionaly, the salt parameter by default contains the string "mnemonic" that is concatenaded with an optional passphrase.

Once again, below another visual representation to make things clear

And guess what? That 512-bit seed can be used to derive child keys using the BIP-32/BIP-44 standard.

7. The role of BIP-44

If you’ve understood the previous BIPs, grasping BIP-44 will be a piece of cake for you.

We saw that in BIP-32, it is technically possible to create an infinite number of derived keys and tree hierarchies. But with all this freedom, things can get messy to the point where it becomes hard to navigate between large trees.

To fix that issue, the missing OG, the infamous BIP-44 standard, proposes a specific path structure that all HD wallets should follow to maintain consistency when importing mnemonic words into wallets.

Below is the path structure:

m / purpose' / coin_type' / account' / change / address_index

purpose' is always set to '44 ( 44 represents the BIP proposal number )

coin_type' is the type of the cryptocurrency coin

for ethereum the coin_type valeu is 60' while for bitcoin is 0'

account' can represent the index of a logical account, butin most wallets the value is 0.

change' is always set to 0 for ethereum

Metamask follow the BIP-44 and the only field that increases when adding a new account is the address_index.
the remaining fields are set with the default values.

So, next time you add a new Ethereum account in MetaMask, remember that behind the scenes, it is deriving a new private key by increasing the address_index value.

The world of wallets is vast, and there’s much more to explore about the technology behind them.
However, this post serves as a solid starting point for those who want to understand the fundamentals or even consider developing their own wallet.


Thank you for taking the time to read this post!
I hope it helped you better understand the concepts discussed.

If you have any questions, feel free to reach out at elizeudev@thecodepal.com, I’m always happy to help!

Stay curious and keep building. See you in the next post pals 😉!